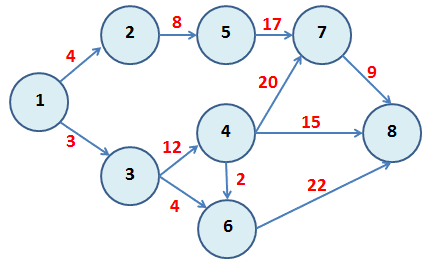
El Problema del Camino más Corto (o ruta más barata) consiste en encontrar una ruta o camino óptimo entre un nodo fuente y un nodo destino, los cuales están enlazados a través de una red con arcos que poseen un cierto atributo, el cual puede ser costo, distancia, tiempo, etc.
La Programación Entera permite abordar de forma eficiente este tipo de problemas, en especial cuando la cantidad de nodos y rutas posibles resulta ser un número significativo. Utilizar en estos casos un enfoque intuitivo de resolución es tedioso y de no ser exhaustivo no garantiza la identificación de la mejor alternativa o ruta.
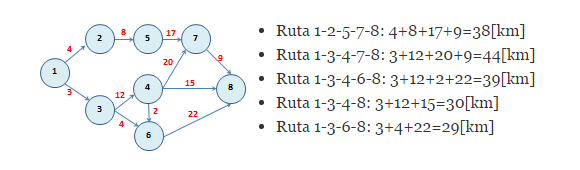
El tamaño reducido de la red anterior permite encontrar el camino más corto simplemente enumerando las distintas alternativas que comenzando en el nodo 1 permita llegar al nodo 8. De esta forma las rutas posibles son:
- Ruta 1-2-5-7-8: 4+8+17+9=38[km]
- Ruta 1-3-4-7-8: 3+12+20+9=44[km]
- Ruta 1-3-4-6-8: 3+12+2+22=39[km]
- Ruta 1-3-4-8: 3+12+15=30[km]
- Ruta 1-3-6-8: 3+4+22=29[km]
La ruta o camino más corto esta dada por la secuencia 1-3-6-8 con una distancia total de 29[km].
A continuación se formula un modelo de Programación Entera que permite extender este tipo de resultados a un problema de estas características:
Variables de Decisión:
Función Objetivo: Minimizar la distancia total en [km] dada por la siguiente expresión:

No hay comentarios.:
Publicar un comentario