Arboles

RUTA MAS CORTA EJERCICIO

LA RUTA MAS CORTA

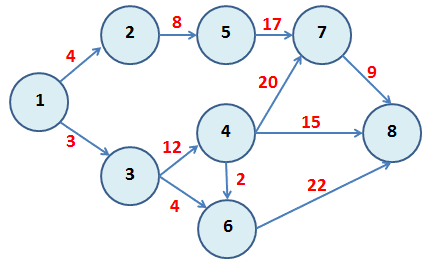
El Problema del Camino más Corto (o ruta más barata) consiste en encontrar una ruta o camino óptimo entre un nodo fuente y un nodo destino, los cuales están enlazados a través de una red con arcos que poseen un cierto atributo, el cual puede ser costo, distancia, tiempo, etc.

La Programación Entera permite abordar de forma eficiente este tipo de problemas, en especial cuando la cantidad de nodos y rutas posibles resulta ser un número significativo. Utilizar en estos casos un enfoque intuitivo de resolución es tedioso y de no ser exhaustivo no garantiza la identificación de la mejor alternativa o ruta.

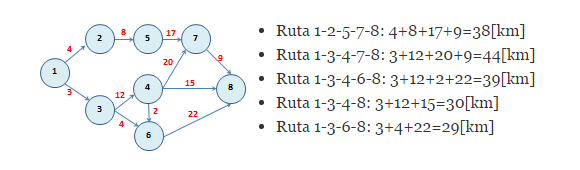
El tamaño reducido de la red anterior permite encontrar el camino más corto simplemente enumerando las distintas alternativas que comenzando en el nodo 1 permita llegar al nodo 8. De esta forma las rutas posibles son:

• Ruta 1-2-5-7-8: 4+8+17+9=38[km]
• Ruta 1-3-4-7-8: 3+12+20+9=44[km]
• Ruta 1-3-4-6-8: 3+12+2+22=39[km]
• Ruta 1-3-4-8: 3+12+15=30[km]
• Ruta 1-3-6-8: 3+4+22=29[km]

La ruta o camino más corto esta dada por la secuencia 1-3-6-8 con una distancia total de 29[km].

A continuación se formula un modelo de Programación Entera que permite extender este tipo de resultados a un problema de estas características:

Variables de Decisión:

Función Objetivo: Minimizar la distancia total en [km] dada por la siguiente expresión:

Grafos foto

Ejercicios de Grafos

Teoría de Grafos

TEORIA DE GRAFOS

La Teoría de Grafos juega un papel importante en la fundamentación matemática de las Ciencias de la Computación. Los grafos constituyen una herramienta básica para modelar fenómenos discretos y son fundamentales para la comprensión de las estructuras de datos y el análisis de algoritmos. En matemáticas y ciencias de la computación, la teoría de grafos estudia las propiedades de los grafos, que son colecciones de objetos llamados vértices (o nodos) conectados por líneas llamadas aristas (o arcos) que pueden tener orientación (dirección asignada). Típicamente, un grafo está diseñado por una serie de puntos (los vértices) conectados por líneas (las aristas).

El trabajo de Leonhard Euler, en 1736, sobre el problema de los puentes de Königsberg es considerado como uno de los primeros resultados de la teoría de grafos. También se considera uno de los primeros resultados topológicos en geometría (que no depende de ninguna medida). Este ejemplo ilustra la profunda relación entre la teoría de grafos y la topología. En 1845 Gustav Kirchhoff publicó sus leyes de los circuitos para calcular el voltaje y la corriente en los circuitos eléctricos.
En 1852 Francis Guthrie planteó el problema de los cuatro colores que plantea si es posible, utilizando solamente cuatro colores, colorear cualquier mapa de países de tal forma que dos países vecinos nunca tengan el mismo color. Este problema, que no fue resuelto hasta un siglo después por Kenneth Appel y Wolfgang Haken, puede ser considerado como el nacimiento de la teoría de grafos. Al tratar de resolverlo, los matemáticos definieron términos y conceptos teóricos fundamentales de los grafos. (Fuente) 

6.1 ELEMENTOS Y CARACTERÍSTICAS DE LOS GRAFOS

Un grafo (G) es un diagrama que consta de un conjunto de vértices (V) y un conjunto de lados (L).
Considérese el siguiente grafo:

A partir de esta figura se definen los siguientes elementos:

Vértices (nodos)
Se indican por medio de un pequeño círculo y se les asigna un número o letra. En el grafo anterior los vértices son V= {a,b,c,d}.

Lados (ramas o aristas)
Son las líneas que unen un vértice con otro y se les asigna una letra, un numero o una combinación de ambos. En el grafo anterior los lados son: L= {1, 2, 3, 4, 5, 6}.

Lados paralelos
Son aquellas aristas que tienen relación con un mismo par de vértices. En el grafo anterior los lados paralelos son: P={2,3}.

Lazo
Es aquella arista que sale de un vértice y regresa al mismo vértice. En el grafo anterior se tiene el lazo: A= {6}

Valencia de un vértice
Es el numero de lados que salen o entran a un vértice. En el grafo anterior las valencias de los vértices son:
Valencia (a)=2
Valencia (b)=4
Valencia (c)=2
Valencia (d)=3
Hay que observar como en el caso del vértice del lazo solo se considera una vez, entrada o salida pero no ambos.

6.1.1 COMPONENTES DE UN GRAFO

Aristas :

Son las líneas con las que se unen las aristas de un grafo y con la que se construyen también caminos. Si la arista carece de dirección se denota indistintamente {a, b} o {b, a}, siendo a y b los vértices que une. Si {a ,b} es una arista, a los vértices a y b se les llama sus extremos.
• Aristas Adyacentes: Se dice que dos aristas son adyacentes si convergen en el mismo vértice.
• Aristas Paralelas: Se dice que dos aristas son paralelas si vértice inicial y el final son el mismo.
• Aristas Cíclicas: Arista que parte de un vértice para entrar en el mismo.
• Cruce: Son dos aristas que cruzan en un punto. 

Vértices :

Son los puntos o nodos con los que esta conformado un grafo. Llamaremos grado de un vértice al número de aristas de las que es extremo. Se dice que un vértice es `par' o `impar' según lo sea su grado.
• Vértices Adyacentes: si tenemos un par de vértices de un grafo (U, V) y si tenemos un arista que los une, entonces U y V son vértices adyacentes y se dice que U es el vértice inicial y V el vértice adyacente.
• Vértice Aislado: Es un vértice de grado cero.
• Vértice Terminal: Es un vértice de grado 1. 

Subir

6.1.2 TIPOS DE GRAFOS

GRAFOS SIMPLES
Son aquellos grafos que no tienen lazos ni lados paralelos.

GRAFO COMPLETO DE N VÉRTICES (kn)
Es el grafo en donde cada vértice está relacionado con todos los demás sin lazos ni lados paralelos. Se indica como kn en donde n es el número de vértices del grafo.

La valencia en cada uno de los vértices de los grafos completos es (n – 1), y el numero de lados esta dado por la expresión
Núm. De lados = n(n – 1)
2
en donde n es el numero de vértices del grafo.

COMPLEMENTO DE UN GRAFO (G‘)
Es el grafo que le falta al grafo G, de forma que entre ambos formas de grafo completo de n vértices. Este grafo no tiene lazos ni ramas paralelas.

GRAFO BIPARTIDO
es el grafo que esta compuesta por dos conjuntos de vértices, A ={a1,a2, a3…, an} y B = {b1,b2,…, bm} en donde los elementos del conjunto B, pero entre los vértices de un mismo conjunto no existe arista que los una.

Una forma muy sencilla de saber si un grafo es bipartido es aplicar el hecho de que nunca tiene un ciclo de longitud impar, además de que debe cumplir con la característica mencionada anteriormente.

GRAFO BIPARTIDO COMPLETO (Kn, m) 
Es el grafo que esta compuesto por dos conjuntos de vértices, uno de ellos A ={a1,a2, a3…, an} Y otro B= {b1,b2,…, bm), y en el cada vértice de A esta unido con todo los vértices de B, pero entre los vértices de un mismo conjunto no existe arista que los una. El grafo bipartido completo se indica como kn, m.

Subir

6.2 REPRESENTACIÓN DE LOS GRAFOS

Matriz de adyacencia

Dado un grafo G = (V, E) con n vértices {v1, ..., vn} su matriz de adyacencia es la matriz de orden n×n, A(G)=(aij) donde aijes el número de aristas que unen los vértices vi y vj. La matriz de adyacencia de un grafo es simétrica. Si un vértice es aislado entonces la correspondiente fila (columna) esta compuesta sólo por ceros. Si el grafo es simple entonces la matriz de adyacencia contiene solo ceros y unos (matriz binaria) y la diagonal esta compuesta sólo por ceros. 

Matriz de incidencia

Dado un grafo simple G = (V, E) con n=|V| vértices {v1, ..., vn} y m=|E| aristas {e1, ..., em}, su matriz de incidencia es la matriz de orden nxm, B(G)=(bij), donde bij=1 si vi es incidente con ej ybij=0 en caso contrario. La matriz de incidencia sólo contiene ceros y unos (matriz binaria). Como cada arista incide exactamente en dos vértices, cada columna tiene exactamente dos unos. El número de unos que aparece en cada fila es igual al grado del vértice correspondiente. Una fila compuesta sólo por ceros corresponde a un vértice aislado.

Subir

6.2.1 MATEMÁTICA

En matemáticas y ciencias de la computación, la teoría de grafos, también llamada teoría de loas graficas estudia las propiedades de los grafos (también llamados graficas) Un grafo es un conjunto, no vacío, de objetos llamados vértices (o nodos) y una selección de partes de vértices llamados aristas. 

Subir

6.2.2 COMPUTACIONAL

Existen diferentes formas de almacenar grafos en una computadora. La estructura de datos, usada depende de las características del grafo y el algoritmo usado para manipularlo. Entre las estructuras mas sencillas y usadas se encuentran las listas y las matrices y aunque frecuentemente se usa una combinación de ambos. 

Subir

6.3 AlGORITMOS DE RECORRIDO Y BUSQUEDA

6.3.1 EL CAMINO MAS CORTO

El problema de los caminos más cortos es el problema que consiste en encontrar un camino entre dos vértices (o nodos) de tal manera que la suma de los pesos de las aristas que lo constituyen es mínima. Ahora bien, podemos emplear el algoritmo de Dijkstra para éstos casos, los pasos o procedimientos a seguir para éste algoritmo son los siguientes : Teniendo un grafo dirigido ponderado de N nodos no aislados, sea x el nodo inicial, un vector D de tamaño N guardará al final del algoritmo las distancias desde x al resto de los nodos. 
1 Inicializar todas las distancias en D con un valor infinito relativo ya que son desconocidas al principio, exceptuando la de x que se debe colocar en 0 debido a que la distancia de x a x sería 0. 
2 Sea a = x (tomamos a como nodo actual). 
3 Recorremos todos los nodos adyacentes de a, excepto los nodos marcados, llamaremos a estos vi 
4 Si la distancia desde x hasta va guardada en D es mayor que la distancia desde x hasta a, sumada a la distancia desde a hasta vi; esta se sustituye con la segunda nombrada. 
5 Marcamos como completo el nodo a. 
6 Tomamos como próximo nodo actual el de menor valor en D (puede hacerse almacenándolos valores en una cola de prioridad) y volvemos al paso 3 mientras existan nodos no marcados. 

Subir

6.3.2 EN LO ANCHO

La búsqueda en anchura es otro procedimiento para visitar sistemáticamente todos los vértices de un grafo. Es adecuado especialmente para resolver problemas de optimización, en los que se deba elegir la mejor solución entre varias posibles. Al igual que en la búsqueda en profundidad se comienza en un vértice v (la raíz) que es el primer vértice activo. En el siguiente paso se etiquetan como visitados todos los vecinos del vértice activo que no han sido etiquetados. Se continúa etiquetando todos los vecinos de los hijos de v (que no hayan sido visitados aún). En este proceso nunca se visita un vértice dos veces por lo que se construye un grafo sin ciclos, que será un árbol

Subir

6.3.3 EN PROFUNDIDAD

En la búsqueda en profundidad se avanza de vértice en vértice, marcando cada vértice visitado. La búsqueda siempre avanza hacia un vértice no marcado, internándose “profundamente” en el grafo sin repetir ningún vértice. Cuando se alcanza un vértice cuyos vecinos han sido marcados, se retrocede al anterior vértice visitado y se avanza desde éste 

Ejercicio de compuertas logicas

Ejersicios de compuertas logicas

Compuertas logicas

Las Compuertas Lógicas son circuitos electrónicos conformados internamente por transistores que se encuentran con arreglos especiales con los que otorgan señales de voltaje como resultado o una salida de forma booleana, están obtenidos por operaciones lógicas binarias (suma, multiplicación). También niegan, afirman, incluyen o excluyen según sus propiedades lógicas. Estas compuertas se pueden aplicar en otras áreas de la ciencia como mecánica, hidráulica o neumática.

Existen diferentes tipos de compuertas y algunas de estas son más complejas, con la posibilidad de ser simuladas por compuertas más sencillas. Todas estas tienen tablas de verdad que explican los comportamientos en los resultados que otorga, dependiendo del valor booleano que tenga en cada una de sus entradas.

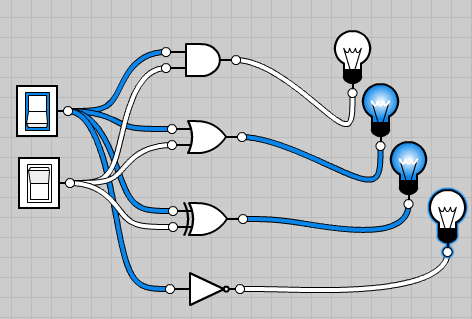
Fig. 1 Compuertas Lógicas

Trabajan en dos estado, “1” o “0”, los cuales pueden asignarse a la lógica positiva o lógica negativa. El estado 1 tiene un valor de 5v como máximo y el estado 0 tiene un valor de 0v como mínimo y existiendo un umbral entre estos dos estados donde el resultado puede variar sin saber con exactitud la salida que nos entregara. Las lógicas se explican a continuación:

• La lógica positiva es aquella que con una señal en alto se acciona, representando un 1 binario y con una señal en bajo se desactiva. representado un 0 binario.
• La lógica negativa proporciona los resultados inversamente, una señal en alto se representa con un 0 binario y una señal en bajo se representa con un 1 binario.

A continuación vamos a analizar las diferentes operaciones lógicas una por una comenzando por la más simple:

Compuerta AND

Esta compuerta es representada por una multiplicación en el Algebra de Boole. Indica que es necesario que en todas sus entradas se tenga un estado binario 1 para que la salida otorgue un 1 binario. En caso contrario de que falte alguna de sus entradas con este estado o no tenga si quiera una accionada, la salida no podrá cambiar de estado y permanecerá en 0. Esta puede ser simbolizada por dos o más interruptores en serie de los cuales todos deben estar activos para que esta permita el flujo de la corriente.

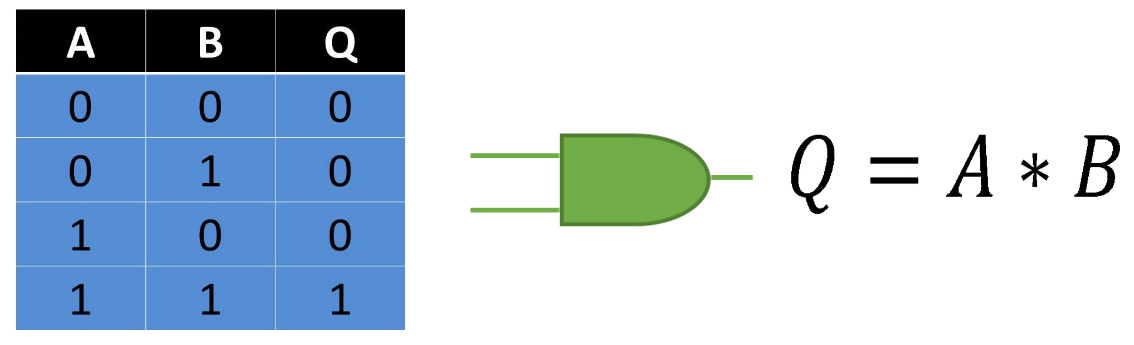
Fig. 2 Tabla, Representación y Fórmula Compuerta AND.

Compuerta OR

En el Algebra de Boole esta es una suma. Esta compuerta permite que con cualquiera de sus entradas que este en estado binario 1, su salida pasara a un estado 1 también. No es necesario que todas sus entradas estén accionadas para conseguir un estado 1 a la salida pero tampoco causa algún inconveniente. Para lograr un estado 0 a la salida, todas sus entradas deben estar en el mismo valor de 0. Se puede interpretar como dos interruptores en paralelo, que sin importar cual se accione, será posible el paso de la corriente.

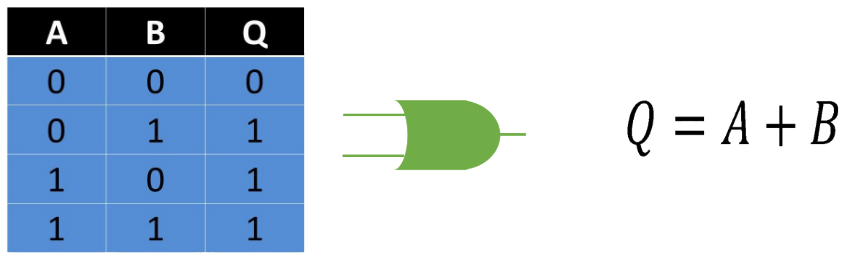
Fig. 3 Tabla, Representación y Fórmula Compuerta OR.

Compuerta NOT

En este caso esta compuerta solo tiene una entrada y una salida y esta actúa como un inversor. Para esta situación en la entrada se colocara un 1 y en la salida otorgara un 0 y en el caso contrario esta recibirá un 0 y mostrara un 1. Por lo cual todo lo que llegue a su entrada, será inverso en su salida.

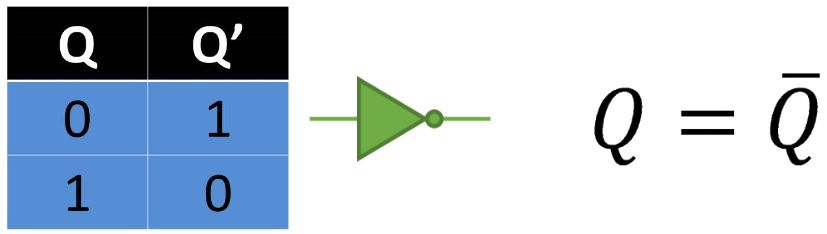
Fig. 4 Tabla, Representación y Fórmula Compuerta NOT.

Compuerta NAND

También denominada como AND negada, esta compuerta trabaja al contrario de una AND ya que al no tener entradas en 1 o solamente alguna de ellas, esta concede un 1 en su salida, pero si esta tiene todas sus entradas en 1 la salida se presenta con un 0.

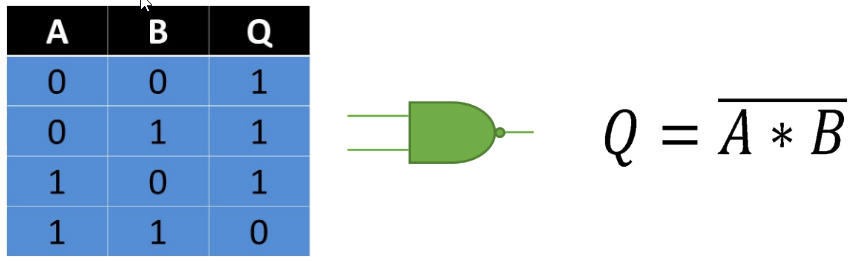
Fig. 5 Tabla, Representación y Fórmula Compuerta NAND.

Compuerta NOR

Así como vimos anteriormente, la compuerta OR también tiene su versión inversa. Esta compuerta cuando tiene sus entradas en estado 0 su salida estará en 1, pero si alguna de sus entradas pasa a un estado 1 sin importar en qué posición, su salida será un estado 0.

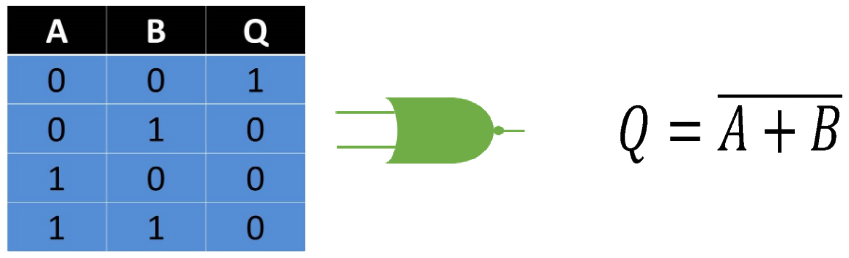
Fig. 6 Tabla, Representación y Fórmula Compuerta NOR.

Compuerta XOR

También llamada OR exclusiva, esta actúa como una suma binaria de un digito cada uno y el resultado de la suma seria la salida. Otra manera de verlo es que con valores de entrada igual el estado de salida es 0 y con valores de entrada diferente, la salida será 1.

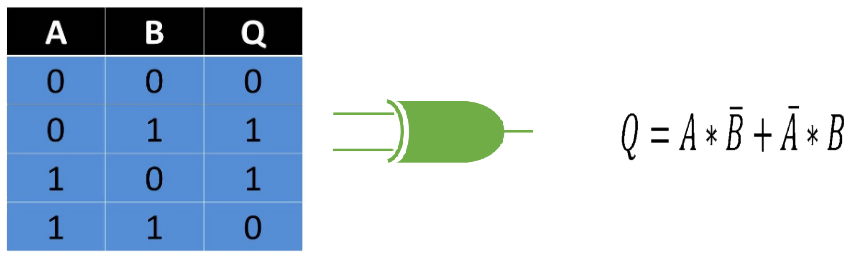
Fig. 7 Tabla, Representación y Fórmula Compuerta XOR.

Compuerta XNOR

Esta es todo lo contrario a la compuerta XOR, ya que cuando las entradas sean iguales se presentara una salida en estado 1 y si son diferentes la salida será un estado 0.

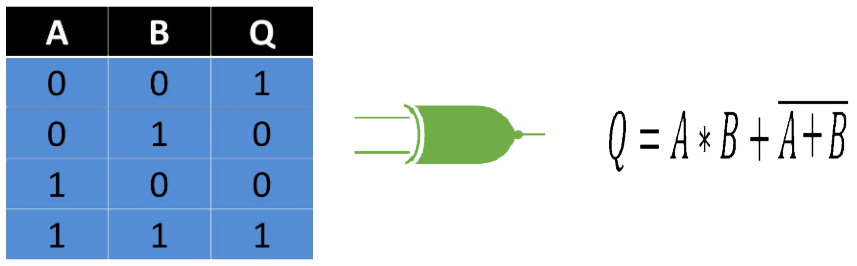
Fig. 8 Tabla, Representación y Fórmula Compuerta XNOR.

Compuerta IF

Esta compuerta no es una muy utilizada o reconocida ya que su funcionamiento en estados lógicos es parecido a si solo hubiera un cable conectado porque exactamente lo que se le coloque en la entrada, se encontrara en la salida. Pero también es conocido como un buffer, en la práctica se utiliza como amplificador de corriente o como seguidor de tensión para adaptar impedancias.

Fig. 9 Tabla, Representación y Fórmula Compuerta IF.